آشنایی با مونت کارلو

خوب، وقتی پویایی مدل محیط  را نمی‌دانیم چگونه می‌توانیم سیاست بهینه را پیدا کنیم  ؟ در چنین مواردی می‌توانیم از روش های بدون مدل استفاده کنیم.

در روش‌های بدون مدل نیازی به دینامیک مدل محیط برای محاسبه مقدار و توابع Q به منظور پیدا کردن سیاست بهینه ندارند . یکی از این روش‌های بدون مدل، روش مونت کارلو (MC) است.

روش مونت کارلو یک روش اماری است که برای یافتن راه حل تقریبی از طریق  نمونه‌برداری  استفاده می‌کند.

روش برنامه نویسی پویا و بلمن

روش مبتنی بر مدل یعنی برای پیدا کردن سیاست بهینه تنها زمانی که پویایی مدل (احتمال انتقال) محیط شناخته شده است کمک خواهند کرد. اگر دینامیک مدل را نداشته باشیم، نمی‌توانیم این روش ها را اعمال کنیم.

یکی از این روش‌ها روش برنامه نویسی پویا (DP) است.

دو روش مهم که با استفاده از DP برای پیدا کردن سیاست بهینه استفاده می‌شوند را معرفی می‌کنیم . دو روش عبارتند از:

·       تکرار ارزش

·       تکرار سیاست

·       تکرار ارزش

در روش تکرار ارزش، سعی می‌کنیم سیاست بهینه را پیدا کنیم. یاد گرفتیم که سیاست بهینه ان است که به عامل می‌گوید که عمل درست را هر حالت به منظور پیدا کردن سیاست بهینه انجام دهد ، ابتدا تابع مقدار بهینه را محاسبه می‌کنیم و هنگامی که تابع ارزش مطلوب، را یافتیم می‌توانیم از ان برای استخراج  سیاست بهینه استفاده کنیم، چگونه می‌توانیم تابع مقدار بهینه را محاسبه کنیم؟ می‌توانیم از معادله بلمن بهینه برای  تابع ارزش استفاده کنیم.

·       تکرارسیاست

این مرحله دقیقا همان چیزی است که تابع مقدار را در روش تکرار ارزش محاسبه کردیم. اما با یک تفاوت کوچک. در اینجا،  تابع ارزش را با استفاده از سیاست محاسبه می‌کنیم اما در روش تکرار ارزش، ارزش را با در نظر گرفتن حداکثر مقادیر Q محاسبه می‌کنیم.

در یادگیری تقویتی، هدف این است که  سیاست بهینه را پیدا کنیم. سیاست بهینه سیاستی است که عمل درست را در هر حالت انتخاب کند به طوری که عامل حداکثر بازگشت برای  رسیدن به هدف داشته باشد.

در این فصل، با دو مفهوم یادگیری تقویتی کلاسیک جالب آشنا خواهیم شد که الگوریتم های روش های تکرار ارزش و سیاست نامیده می‌شوند که می‌توانیم از ان برای پیدا کردن سیاست بهینه استفاده کنیم.

قبل از ورود به روش‌های تکرار ارزش و سیاست به طور مستقیم، ابتدا، معادله بلمن را یاد خواهیم گرفت. معادله Bellman در یادگیری تقویتی همه جا حاضر است واز ان برای پیدا کردن مقدار بهینه و توابع Q استفاده می‌شود. ابتدا ببینیم  که معادله بلمن چیست و چگونه سیاست بهینه و توابع Q را پیدا می‌کند.

 پس از آشنایی با معادله بلمن، روش‌های برنامه نویسی پویا به نام تکرار ارزش و سیاست، که از معادله بلمن برای پیدا کردن سیاست بهینه استفاده می‌کنند را بررسی خواهیم کرد .

تابع مقدار(Value) و تابع Q

تابع مقدار

تابع مقدار، همچنین تابع مقدار حالت نامیده می‌شود، که نشان‌دهنده ارزش حالت است. ارزش یک حالت، بازگشتی ( مقدار پاداشی) است که یک عامل از ان حالت با پیروی از سیاست π به دست می‌اورد. مقدار یک حالت یا تابع مقدار معمولا با V(s) مشخص می‌شود و می‌توان ان را به این شکل بیان کرد:

که در ان s0 = s به این معنی است که حالت شروع s است. ارزش مقدار یک state نامیده می‌شود. 

یادگیری و انواع آن

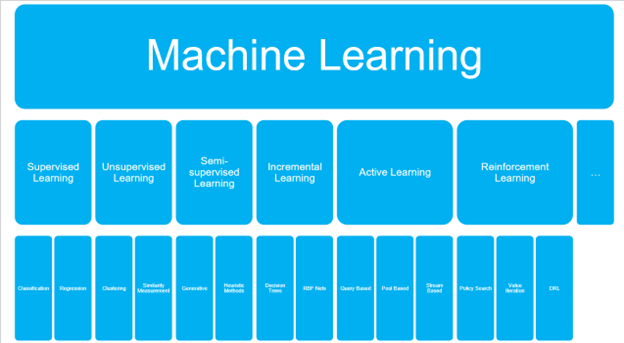
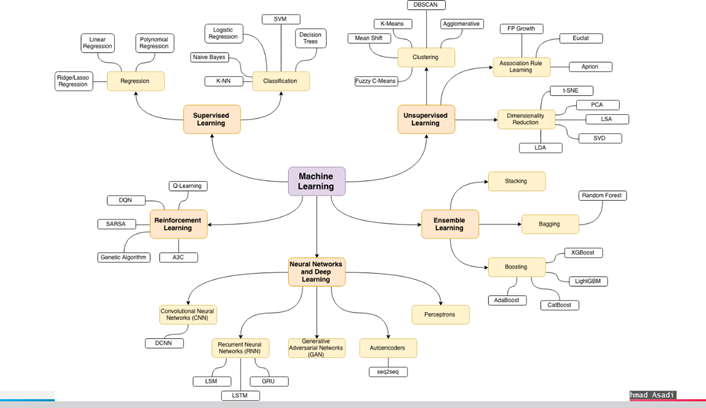
یادگیری ماشین  شامل چهار شاخه است که عبارتند از:

 1-یادگیری با ناظر 

2- یادگیری بدون ناظر 

3- یادگیری نیمه نظارتی

4- یادگیری تقویتی 

لذا  یادگیری تقویتی (RL) یکی از زمینه های یادگیری ماشین (ML) است. بر خلاف سایر پارادایم های ML، مانند یادگیری تحت نظارت و بدون نظارت، داده‌ها  در RL در یک مد ازمون و خطا ، از طریق تعامل با محیط خود جمع آوری می گردند.

RL یکی از فعال ترین زمینه های تحقیق در هوش مصنوعی است و اعتقاد بر این است که RL ما را یک گام به سمت دستیابی به عمومی شدن هوش مصنوعی نزدیک تر می‌کند . RL به سرعت در چند سال گذشته با طیف گسترده ای از برنامه های کاربردی اعم از ساخت  سیستم های اتومبیل های خودران تکامل یافته است.

دلیل اصلی این تکامل ظهور یادگیری تقویتی عمیق است که ترکیبی از یادگیری عمیق و RL است. با ظهور الگوریتم‌ها و کتابخانه‌های جدید  یادگیری تقویتی ، این یادگیری  به وضوح یکی از امیدوار کننده ترین قسمت‌های یادگیری ماشین است.

در یادگیری تحت نظارت، ماشین از داده های اموزشی یاد می‌گیرد. داده های اموزشی شامل یک جفت برچسب ورودی و خروجی است. بنابراین، ما مدل (عامل) را با استفاده از داده های اموزشی اموزش می‌دهیم به گونه ای که مدل می‌تواند یادگیری خود را به اطلاعات جدید دیده نشده تعمیم دهد. این یادگیری تحت نظارت نامیده می‌شود زیرا داده‌های اموزشی به عنوان یک ناظر، که دارای جفت برچسب ورودی و خروجی است و مدل را هدایت می کند.

آشنایی با فرایند مارکوف

                فرایندهای تصمیم‌گیری مارکوف

فرایند تصمیم‌گیری مارکوف (MDP) یک چارچوب ریاضی برای حل مسائل RL است. تقریبا تمام مسائل RL را می‌توان به عنوان یک MDP مدل سازی کرد. MDP ها به طور گسترده ای برای حل مسائل مختلف بهینه سازی استفاده می‌شود. در این بخش، بررسی می‌کنیم که MDP چیست و چگونه در RL استفاده می‌شود.

برای درک MDP، ابتدا باید خصوصیات مارکوف و حلقه مارکوف را یاد بگیریم.

 خصوصیات مارکوف و حلقه مارکوف

خصوصیات مارکوف می‌گوید که اینده فقط به زمان حال بستگی دارد و نه به گذشته. همچنین زنجیره مارکوف، به عنوان فرایند مارکوف شناخته می‌شود، و شامل یک توالی حالتهایی است که به شدت از خصوصیات مارکوف پیروی می‌کنند؛ یعنی زنجیره مارکوف مدل احتمالاتی است که تنها به وضعیت فعلی بستگی دارد تا وضعیت بعدی را پیش بینی کند. یعنی اینده به طور مشروط مستقل از گذشته است.

به عنوان مثال، اگر می‌خواهیم اب و هوا را پیش بینی کنیم و می‌دانیم که وضعیت فعلی ابری است ، می‌توانیم پیش بینی کنیم که حالت بعدی می‌تواند بارانی باشد. به این نتیجه رسیدیم که حالت بعدی به احتمال زیاد تنها با در نظر گرفتن وضعیت فعلی (ابری) بارانی است  و به حالتهای قبلی، که ممکن است افتابی، باد و غیره باشد بستگی ندارد.

با این حال، خصوصیات مارکوف برای همه فرایندها مناسب نیست. به عنوان مثال، در پرتاب یک تاس (حالت بعدی) هیچ وابستگی به شماره قبلی ندارد که در تاس (وضعیت فعلی) نشان داده شده است.