آشنایی با فرایند مارکوف

                فرایندهای تصمیم‌گیری مارکوف

فرایند تصمیم‌گیری مارکوف (MDP) یک چارچوب ریاضی برای حل مسائل RL است. تقریبا تمام مسائل RL را می‌توان به عنوان یک MDP مدل سازی کرد. MDP ها به طور گسترده ای برای حل مسائل مختلف بهینه سازی استفاده می‌شود. در این بخش، بررسی می‌کنیم که MDP چیست و چگونه در RL استفاده می‌شود.

برای درک MDP، ابتدا باید خصوصیات مارکوف و حلقه مارکوف را یاد بگیریم.

 خصوصیات مارکوف و حلقه مارکوف

خصوصیات مارکوف می‌گوید که اینده فقط به زمان حال بستگی دارد و نه به گذشته. همچنین زنجیره مارکوف، به عنوان فرایند مارکوف شناخته می‌شود، و شامل یک توالی حالتهایی است که به شدت از خصوصیات مارکوف پیروی می‌کنند؛ یعنی زنجیره مارکوف مدل احتمالاتی است که تنها به وضعیت فعلی بستگی دارد تا وضعیت بعدی را پیش بینی کند. یعنی اینده به طور مشروط مستقل از گذشته است.

به عنوان مثال، اگر می‌خواهیم اب و هوا را پیش بینی کنیم و می‌دانیم که وضعیت فعلی ابری است ، می‌توانیم پیش بینی کنیم که حالت بعدی می‌تواند بارانی باشد. به این نتیجه رسیدیم که حالت بعدی به احتمال زیاد تنها با در نظر گرفتن وضعیت فعلی (ابری) بارانی است  و به حالتهای قبلی، که ممکن است افتابی، باد و غیره باشد بستگی ندارد.

با این حال، خصوصیات مارکوف برای همه فرایندها مناسب نیست. به عنوان مثال، در پرتاب یک تاس (حالت بعدی) هیچ وابستگی به شماره قبلی ندارد که در تاس (وضعیت فعلی) نشان داده شده است. 

 حرکت از یک حالت به حالت دیگر انتقال نامیده می شود و احتمال وقوع  ان  احتمال انتقال نامیده می‌شود. احتمال انتقال را با استفاده از P(s’ | s). نشان می دهیم که نشاندهنده‌ی احتمال حرکت از حالت s به حالت’ s بعدی است. فرض کنید سه تا حالت (ابری، بارانی و بادی) در زنجیره مارکوف داریم. می‌توانیم  احتمال انتقال از یک حالت به حالت دیگر را  با استفاده از جدولی به نام جدول مارکوف نشان دهیم، همانطور که در جدول 1.1 نشان داده شده است

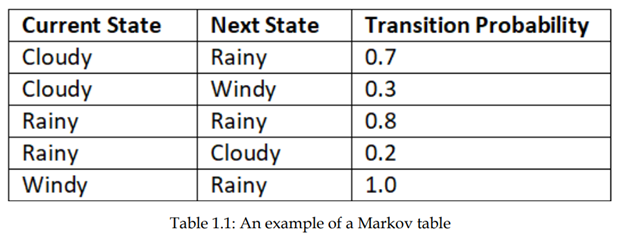
از جدول 1.1 می توانیم مشاهده کنیم که:

از حالت ابری، احتمال انتقال به حالت بارانی 70٪ و به حالت باد با احتمال 30٪ است.

از حالت بارانی، احتمال انتقال به همان حالت بارانی 80٪ او به حالت ابری با احتمال 20٪ است.

از حالت باد، احتمال انتقال به حالت بارانی 100٪ است.

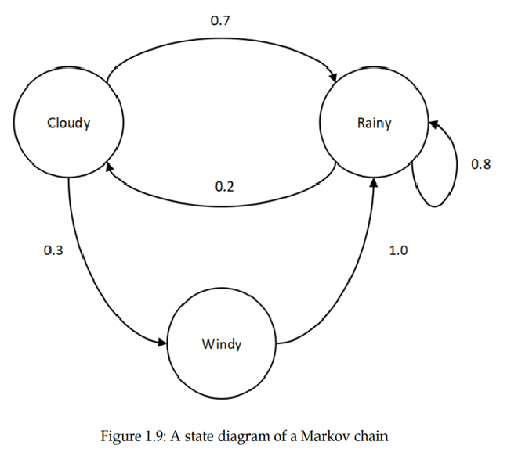
اطلاعات انتقال زنجیره مارکوف را به شکل یک نمودار حالت، همانطور که در شکل 1.9 نشان داده شده است نیز می‌توان نشان داد:

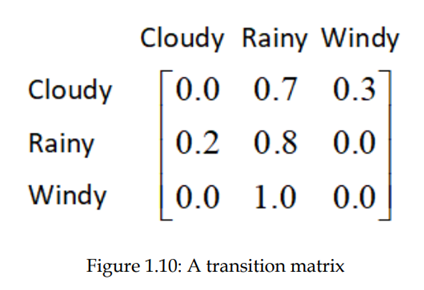
همچنین می‌توانیم احتمالات انتقال را به یک ماتریس به نام transition فرموله کنیم. ماتریس، مانند آنچه در شکل 1.10 نشان داده شده است:

بنابراین، برای نتیجه‌گیری، می‌توانیم بگوییم که زنجیره مارکوف یا فرایند مارکوف شامل مجموعه‌ای از حالتها همراه با احتمالات انتقال خود است.

 فرایند پاداش مارکوف

فرایند پاداش مارکوف (MRP) گسترش زنجیره مارکوف با عملکرد پاداش است. به عبارت دیگر، یاد گرفتیم که زنجیره مارکوف شامل حالت‌ها و احتمال انتقال است. MRP شامل حالت‌ها، احتمال انتقال و همچنین  تابع پاداش است.

تابع پاداش می‌گوید که در هر حالت چه پاداشی به دست می‌آوریم. تابع پاداش معمولا با R (s) مشخص می‌شود. بنابراین، MRP شامل حالت‌های s، احتمال انتقال P(s’ | s). و تابع پاداش R(s) است.

 فرایند تصمیم‌گیری مارکوف

فرایند تصمیم‌گیری مارکوف (MDP) گسترش MRP با اقدامات است. یاد گرفتیم که MRP شامل حالت‌ها، احتمال انتقال و تابع پاداش است. MDP شامل حالت‌ها، احتمال انتقال، تابع پاداش و همچنین فعالیت ها است. خصوصیات مارکوف بیان می‌کند که حالت بعدی فقط به وضعیت فعلی بستگی دارد و بر اساس وضعیت قبلی نیست.

ایا خصوصیات مارکوف قابل اجرا برای  RL است؟

جواب بله است! زیرا در محیط RL، تصمیم‌گیری عامل فقط بر اساس وضعیت فعلی انجام می‌شود و نه بر اساس حالت‌های گذشته. بنابراین می‌توانیم یک محیط RL را به عنوان یک MDP مدل کنیم.

بیایید این را با یک مثال بهتر درک کنیم. ، همان دنیای شبکه را در نظر بگیریم محیطی که قبلا یاد گرفتیم شکل 1.11 محیط شبکه را نشان می‌دهد و هدف عامل این است که از حالت A به حالت I برسد بدون اینکه به  حالت‌های سایه دار سر بزند.

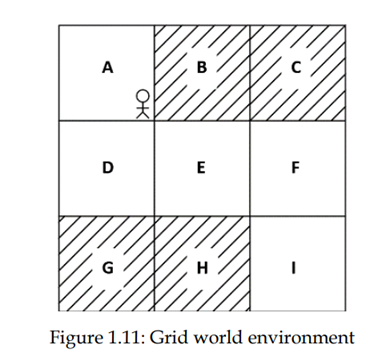
یک عامل تصمیم‌گیری (عمل) را در محیط تنها بر اساس جایی که الان هست انجام می‌دهد و نه بر اساس حالتی که قبلا بوده است. بنابراین، می‌توانیم این  محیط را به عنوان یک MDP فرموله کنیم. یاد گرفتیم که MDP شامل حالت‌ها، اقدامات، احتمالات انتقال و یک تابع پاداش است. حالا، بیایید ببینیم که چگونه با محیط RL این ارتباط برقرار است.

حالتها - مجموعه ای از حالتهای موجود در محیط است که در دنیای شبکه مورد نظر حالت‌ها از A به I هستند.

اقدامات (Actions)– مجموعه‌ای از اقداماتی است که عامل می‌تواند در هر حالت انجام دهد. عامل یک عمل را انجام می‌دهد و از یک حالت به حالت دیگر حرکت می‌کند. در دنیای محیط شبکه ، مجموعه‌ای از اقدامات بالا، پایین، چپ و راست است.

احتمال انتقال - احتمال انتقال با P(s’ | s , a). نشان داده می‌شود. که احتمال حرکت از حالت s به حالت بعدی s’ رابا انجام یک عمل A  نشان می‌دهد. در MRP، احتمال انتقال فقط P(s’ | s)  است و شامل اقدامات نیست. ولی در MDP، شامل اقدامات نیز هست و در نتیجه احتمال انتقال توسط P(s’| s , a) نشان داده شده است.

به عنوان مثال، در محیط شبکه، احتمال انتقال حرکت از حالت A به حالت B در حالی که انجام یک عمل به سمت راست 100٪ است.  می‌تواند به صورت  P(B|A, right) = 1.0 نوشته شود. همچنین می‌توانیم در نمودار حالت هم مشاهده کنیم، همانطور که در شکل 1.12 نشان داده شده است:

 

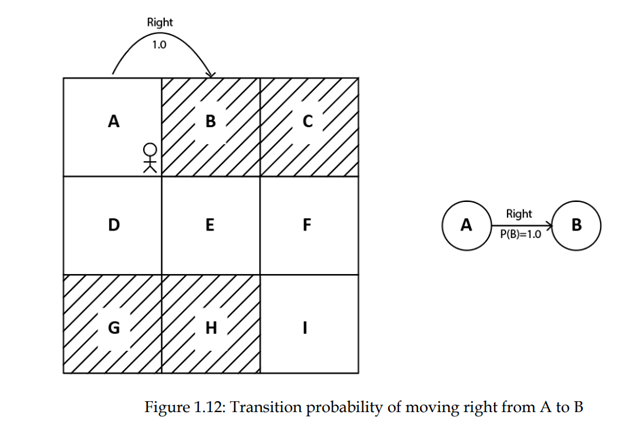
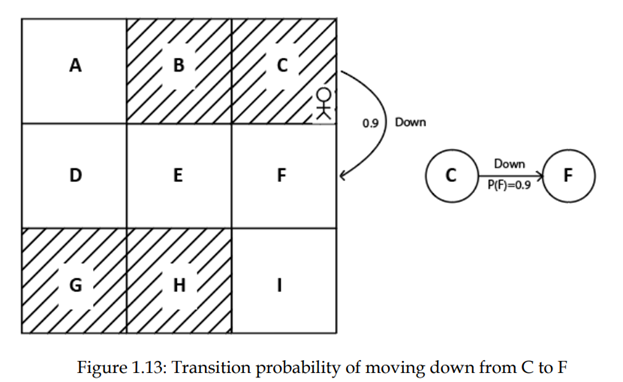
فرض کنید عامل در حالت C قرار دارد و احتمال انتقال حرکت از حالت C به حالت F در حالی که انجام عمل به سمت پایین احتمالش 90٪ است وجود دارد. می توان ان را به این صورت نوشت:

P(F|C, down) = 0.9.

همچنین می‌توانیم این را در نمودار وضعیت مشاهده کنیم، همانطور که در شکل 1.13 نشان داده شده است.

تابع پاداش - تابع پاداش با  R(s,a,s’) مشخص می‌شود. این نشان می‌دهد که عامل با حرکت از حالت s به حالت s’  با انجام عمل a  پاداش به دست اورده است.

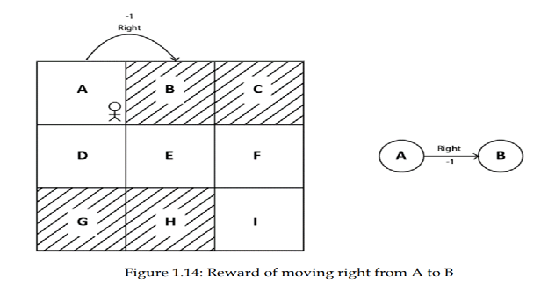
 در صورتی که از وضعیت A به حالت B منتقل می‌شویم، پاداشی را که به دست می‌اوریم منفی باشد، ان را اینگونه بیان می کنند.

R(A, right, B) = -1

همچنین می‌توانید این را در نمودار حالت مشاهده کنید، همانطور که در شکل 1.14 نشان داده شده است:

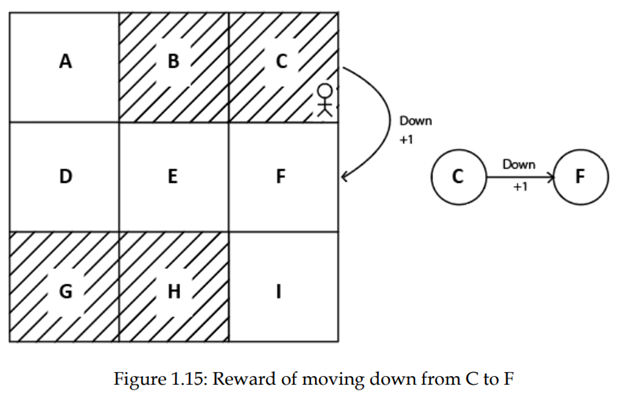
فرض کنید عامل ما در حالت C است و پاداش در انتقال از حالت C به حالت F با انجام عمل پایین +1 است، پس می‌تواند اینگونه بیان شود:

R(C, down, F) = +1

همچنین می‌توانیم این را در نمودار حالت مشاهده کنیم، همانطور که در شکل 1.15 نشان داده شده است:

بنابراین، یک محیط RL را می‌توان به عنوان یک MDP با حالتها، اقدامات، احتمال انتقال و تابع پاداش نشان داد.

 اما صبر کنید! نمایش محیط RL با استفاده از  MDP چه فایده ای دارد؟

می توانیم مشکل RL را به راحتی هنگامی که محیط خود را به عنوان MDP مدل می‌کنیم حل کنیم.. به عنوان مثال، هنگامی که محیط شبکه را با استفاده از MDP، مدل می‌کنیم به راحتی می‌توانیم چگونگی رسیدن به هدف حالت  I از حالت A بدون بازدید از حالت‌های سایه دار را پیدا کنیم.

منبع:

,Deep_Reinforcement_Learning_With_Python_Master_Classic_Rl,_Deep , 

Sudharsan  Ravichandiran,2020