الگوریتم SARSA

در روش کنترل ، هدف پیدا کردن سیاست بهینه است، بنابراین با یک سیاست تصادفی اولیه شروع خواهیم کرد و سپس سعی خواهیم کرد که سیاست بهینه را به صورت تکراری پیدا کنیم.

در فصل قبلی، یاد گرفتیم که روش کنترل را می توان به دو دسته  طبقه بندی کرد :

·       کنترل سیاست On-policy control  ))

·       خارج از سیاست Off-policy control ))

در فصل قبلی یاد گرفتیم که کنترل سیاست و خارج از سیاست به چه معناست. در کنترل سیاست، عامل با استفاده از یک سیاست رفتار می‌کند و برای بهبود همان سیاست تلاش  می‌کند. یعنی در این نوع سیاست،  قسمتها را با استفاده از یک سیاست تولید می‌کنیم و همان سیاست را به طور تکراری برای پیدا کردن سیاست بهینه  بهبود می‌دهیم.

 در روش کنترل خارج از سیاست، عامل با استفاده از یک سیاست رفتار می‌کند و سعی می‌کند سیاست دیگری را بهبود بخشد. به این معنا است که، در روش خارج از سیاست، قسمتها را با استفاده از یک سیاست تولید می‌کنیم و سعی می‌کنیم یک سیاست متفاوت را برای پیدا کردن سیاست بهینه بهبود دهیم.

در حال حاضر، یاد خواهیم گرفت که چگونه وظایف کنترلی را با استفاده از یادگیری TD انجام دهیم. اول، درباره چگونگی کنترل TD را با کنترل سیاست و سپس در مورد خارج از سیاست توضیح خواهیم داد.

  کنترل TD در سیاست – SARSA

در این بخش، به الگوریتم کنترل TD در سیاست به نام SARSA مخفف State-Action-Reward-State-Action نگاه خواهیم کرد . می‌دانیم که در کنترل TD   هدف پیدا کردن سیاست بهینه است. اول، باید ببینیم که چگونه می‌توانیم یک سیاست را استخراج کنیم؟

می‌توانیم سیاست را از تابع Q استخراج کنیم. به عبارت دیگر، هنگامی که تابع Q را داریم پس می‌توانیم سیاست را با انتخاب عمل در هر حالت که حداکثر ارزش  Q را به ما می‌دهد، بدست آوریم.

خوب، چگونه می‌توانیم تابع Q را در یادگیری TD محاسبه کنیم؟ اول، باید به خاطر بیاوریم که چگونه تابع Value را محاسبه کردیم. در یادگیری TD، تابع مقدار از رابطه زیر محاسبه می‌شود:

می توانیم این قانون به روز رسانی را از نظر تابع Q به شکل زیر بازنویسی کنیم:

در حال حاضر، تابع Q را با استفاده از قانون به روز رسانی یادگیری TD قبلی محاسبه می‌کنیم، و سپس یک سیاست را از انها استخراج می‌کنیم. قانون به روز رسانی قبلی را به عنوان قانون به روز رسانی SARSA نامگذاری می‌کنیم.

اما صبر کنید! در روش پیش بینی، یک سیاست به عنوان ورودی برای عمل در  محیط با استفاده از این سیاست و محاسبه تابع ارزش داده شد. اما در اینجا، سیاست را به عنوان ورودی نداریم. چگونه می‌توانیم در محیط عمل کنیم؟

بنابراین، ابتدا تابع Q را با مقادیر تصادفی یا با صفر مقداردهی اولیه می‌کنیم. سپس از این تابع Q که به طور تصادفی مقداردهی اولیه شده است در محیط عمل کرده و سیاست را استخراج می‌کنیم.

سیاست اولیه قطعا مطلوب نخواهد بود زیرا تابع Q اولیه به طور تصادفی است که سیاست از ان استخراج می‌شود، اما در هر قسمت، تابع Q  را به روز می‌کنیم . بنابراین، در هر قسمت، می‌توانیم از تابع Q به روز شده برای استخراج یک سیاست جدید استفاده کنیم . بنابراین، سیاست بهینه را پس از انجام یک سری قسمتها به دست خواهیم اورد.

یک نکته مهم که باید به ان توجه کنیم این است که در روش SARSA، به جای استفاده از سیاست حریصانه از سیاست حریصانه اپسیلون استفاده می‌کنیم. به این معنا است که، در یک سیاست حریصانه، همیشه اقدامی را انتخاب می‌کنیم که حداکثر مقدار Q را دارد. اما، در سیاست حریصانه اپسیلون یک عمل تصادفی با احتمال اپسیلون را انتخاب می‌کنیم و بهترین عمل (عمل با حداکثر مقدار Q  ) را با احتمال1-اپسیلون  انتخاب می‌کنیم .

قبل از نگاه مستقیم به الگوریتم، برای درک بهتر، اول، بیایید به صورت دستی محاسبه کنیم و ببینیم که دقیقا چگونه تابع Q (مقدار Q) ) با  استفاده از قانون به روز رسانی SARSA تخمین زده می‌شود و اینکه چگونه می‌توانیم سیاست بهینه را پیدا کنیم.

بیایید همان محیط دریاچه یخ زده را در نظر بگیریم. ابتدا، مقداردهی اولیه جدول Q (تابع) Q با مقادیر تصادفی را انجام می‌دهیم. شکل 5.9 محیط دریاچه یخ زده همراه با جدول Q حاوی مقادیر تصادفی را نشان می‌دهد.

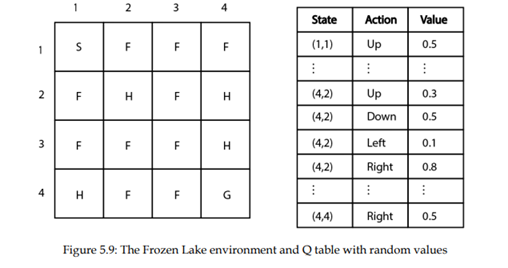
فرض کنید در حالت (4،2). هستیم. حالا  باید یک عمل را در این حالت انتخاب کنیم. چگونه می‌توانیم یک عمل را انتخاب کنیم؟

یاد گرفتیم که در روش SARSA، یک عمل را بر اساس سیاست حریصانه اپسیلون انتخاب می‌کنیم . با احتمال اپسیلون، یک عدد تصادفی را انتخاب می‌کنیم و  عمل را انجام می‌دهیم (بهترین عمل، عملی است که حداکثر مقدار Q را بدهد).

فرض کنید احتمال 1-اپسیلون را انتخاب کنیم. در حالت (4.2)، به سمت راست حرکت می‌کنیم زیرا دارای بالاترین مقدار Q در مقایسه با اقدامات دیگراست، همانطور که در اینجا نشان داده شده است:

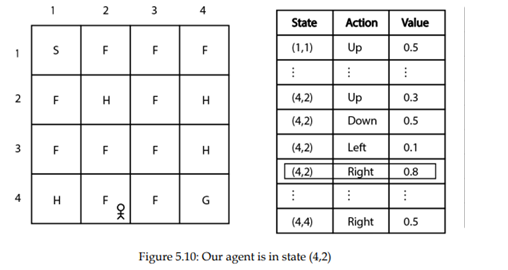
خوب، با انجام عمل راست در حالت (4.2) و حرکت به حالت بعدی (4.3) می‌رویم که در شکل 5.11 نشان داده شده است.

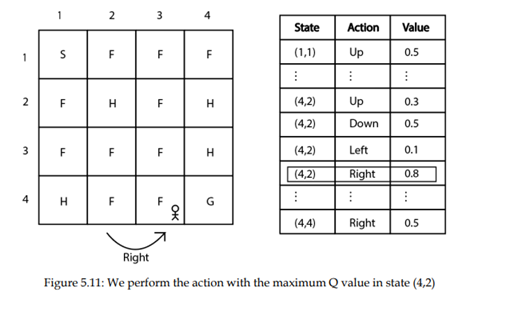
بنابراین، به سمت راست از حالت (4.2) به حالت بعدی (4.3) حرکت کردیم و پاداش 0  دریافت کردیم.بیایید نرخ یادگیری  را 0.1 و ضریب تخفیف گاما را در 1 نگه داریم. چگونه می توانیم مقدار Qرا به روز رسانی کنیم؟

اجازه دهید قانون به روز رسانی SARSA را به یاد بیاوریم:

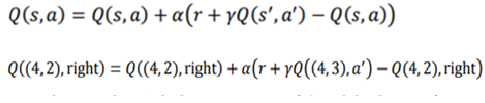
برای محاسبه مقادیر را به صورت زیر فرض کردیم:

r=0 , α= 0.1 , γ= 1

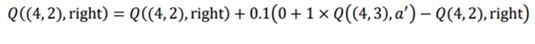
از انجا که به حالت بعدی (4.3) نقل مکان کرده‌ایم، باید یک عمل را در این حالت به منظور محاسبه مقدار Q جفت بعدی state-action انتخاب کنیم. بنابراین، از همان سیاست اپسیلون حریصانه برای انتخاب عمل استفاده می کنیم . یعنی یک عمل تصادفی را با احتمال اپسیلون انتخاب می‌کنیم ، و بهترین عمل را انتخاب می کنیم که حداکثر مقدار Q  با  احتمال 1-اپسیلون را دارد.

فرض کنید از احتمال  اپسیلون استفاده می‌کنیم و عمل تصادفی را انتخاب می‌کنیم. در حالت (4،3)، عمل راست را به طور تصادفی انتخاب می‌کنیم، همانطور که شکل 5.12 نشان می دهد. همانطور که می بینید، چون عمل راست حداکثر مقدار Q را دارد، ان را با احتمال اپسیلون انتخاب کردیم.

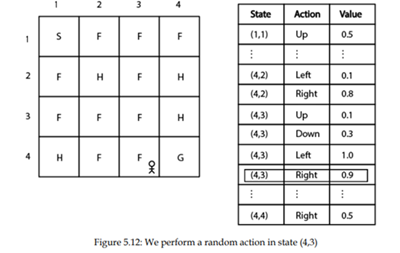
بنابراین، به این ترتیب، تابع Q را با به روز رسانی مقدار Q جفت حالت در هر مرحله از قسمت به روز می‌کنیم. پس از اتمام یک قسمت، یک سیاست جدید از تابع Q به روز شده را استخراج می‌کنیم و از این سیاست جدید برای عمل در محیط استفاده می‌نماییم. (به یاد داشته باشید که سیاست ما همیشه یک سیاست حریصانه اپسیلون است). این مراحل را برای چندین قسمت تکرار می‌کنیم تا سیاست بهینه را پیدا کنیم.

منبع:

Deep_Reinforcement_Learning_With_Python_Master_Classic_Rl,_Deep , 

Sudharsan  Ravichandiran,2020