تابع مقدار(Value) و تابع Q

تابع مقدار

تابع مقدار، همچنین تابع مقدار حالت نامیده می‌شود، که نشان‌دهنده ارزش حالت است. ارزش یک حالت، بازگشتی ( مقدار پاداشی) است که یک عامل از ان حالت با پیروی از سیاست π به دست می‌اورد. مقدار یک حالت یا تابع مقدار معمولا با V(s) مشخص می‌شود و می‌توان ان را به این شکل بیان کرد:

که در ان s0 = s به این معنی است که حالت شروع s است. ارزش مقدار یک state نامیده می‌شود. 

 بیایید تابع ارزش را با یک مثال  بهتردرک کنیم. فرض کنیم که مسیر τ را با سیاست π در محیط شبکه تولید می‌کنیم ، همانطور که در شکل 1.26 نشان داده شده است:

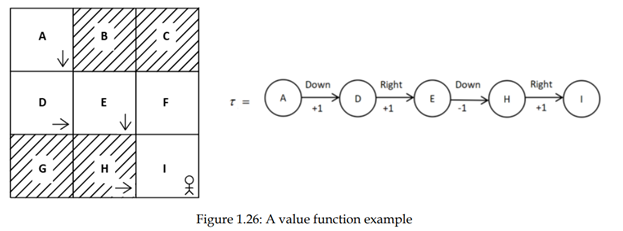
حالا، چگونه ارزش تمام حالت ها را در مسیر خود محاسبه کنیم؟  می توانیم بگوییم که ارزش یک حالت بازگشت (مجموع پاداش) مسیری که از ان حالت شروع می شود و تحت سیاست π تا اخرادامه دارد.

مقدار حالت A بازگشت مسیری است که از حالت A شروع می شود. بنابراین V(A) = 1+1+ -1+1 = 2.

مقدار حالت D بازگشت مسیری است که از حالت D شروع می شود. بنابراین V(D) = 1-1+1= 1.

مقدار حالت E بازگشت مسیری است که از حالت E شروع می شود. بنابراین V(E) = -1+1 = 0.

مقدار حالت H بازگشت مسیری است که از حالت H شروع می شود. بنابراین V(H) = 1.

در مورد ارزش حالت نهایی I چطور؟ یاد گرفتیم که ارزش یک حالت بازگشت (پاداش) از این حالت شروع می شود است. می‌دانیم که وقتی پاداش می‌گیریم از یک حالت به حالت دیگر منتقل می‌شویم. از انجا که I حالت نهایی است، هیچ انتقال از حالت نهایی نداریم، بنابراین هیچ پاداشی وجود ندارد و بنابراین هیچ ارزشی برای حالت I نهایی وجود ندارد.

به طور خلاصه، ارزش یک حالت بازگشت مسیری است که از ان حالت شروع می شود.

صبر کن! یک تغییر کوچک در اینجا وجود دارد: به جای در نظر گرفتن بازگشت به طور مستقیم از مقدارحالت از بازگشت مورد انتظار استفاده خواهیم کرد. لذا در تابع مقدار و مقدار حالت نیز می‌توانیم از بازگشت مورد انتظار که عامل با شروع از حالت s و پیروی از سیاست π بدست آورده است استفاده کنیم. می توان ان را به این شکل بیان کرد:

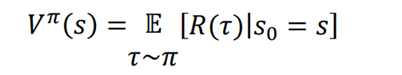
سوال این است که چرا انتظار بازگشت وجود دارد؟

 چرا نمی‌توانیم فقط مقدار یک حالت را به عنوان بازگشت مستقیم محاسبه کنیم ؟

چون بازگشت متغیر تصادفی است و مقادیر مختلف با برخی از احتمالات  طول می‌کشد.

بیایید این را با یک مثال ساده بهتر درک کنیم. فرض کنید یک سیاست تصادفی π داشته باشیم. اموخته ایم  که بر خلاف سیاست قطعی، که نقشه حالت به عامل به طور مستقیم دیکته می‌شود، در سیاست تصادفی اقدامات را بر اساس توزیع احتمال انتخاب می‌کند.

فرض کنید در حالت A هستیم و سیاست تصادفی احتمال توزیع را در فضای عمل را به صورت [0.0،0.80،0.00،0.20]. برمی‌گرداند. این بدان معنی است که با سیاست تصادفی، درحالت  A، عمل انتخاب پایین را در 80٪ از زمان انجام می‌دهیم، یعنی، π(down|A) = 0.8، و عمل انتخاب راست را در  20٪ از زمان، که π(right|A) = 0.20 است.

ابتدا، قسمت τ1 را با استفاده از سیاست تصادفی π تولید می کنیم، همانطور که در شکل 1.27 نشان داده شده است :

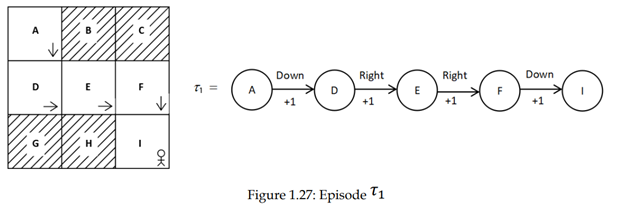
برای درک بهتر، بیایید فقط بر ارزش حالت A تمرکز کنیم. ارزش حالت A بازگشت (مجموع پاداش) مسیری است که از حالت A شروع می‌شود. بنابراین V(A) = R(τ1) =1+1+1+1=4

فرض کنید  قسمت دوم τ2 را با استفاده از همان سیاست تصادفی داده شده π تولید می‌کنیم، مانند آنچه درشکل 1.28 نشان داده شده است:.

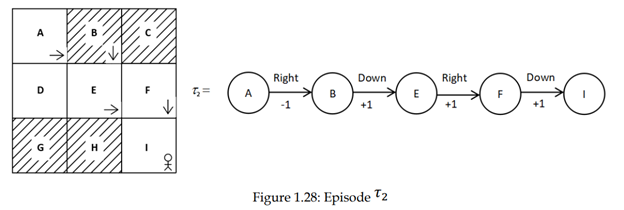
مقدار حالت A بازگشت (مجموع پاداش) مسیر از حالت A است. بنابراین، V(A) = R(τ2) = -1 + 1 + 1 + 1 = 2.

همانطور که مشاهده می‌کنید، اگر چه ما از همان سیاست استفاده می‌کنیم، ارزش های حالت A درمسیرهای τ1 و τ2 متفاوت هستند. این به این دلیل است که سیاست ما یک سیاست تصادفی است و انجام عمل پایین در حالت A را در 80٪ از زمان و انتخاب عمل راست در این حالت را در 20 درصد از زمان اانتخاب می‌کند. بنابراین، هنگامی که یک مسیر را با استفاده از سیاست π تولید می‌کنیم، مسیر τ1، 80 درصد از زمان رخ خواهد داد و مسیر τ2 در 20 درصد از زمان رخ خواهد داد. بنابراین، بازگشت 4 برای 80٪ از زمان و 2 برای 20٪ از زمان خواهد بود.

بنابراین، به جای در نظر گرفتن ارزش حالت که به طور مستقیم بازمی‌گردد، بازده مورد انتظار، که ازبازگشت مقادیر مختلف با برخی از احتمالات است را در نظر می‌گیریم.  بازده مورد انتظار اساسا میانگین وزنی است، یعنی مجموع بازده بر اساس احتمال انها ضرب می‌شود. بنابراین می‌توانیم بنویسیم:

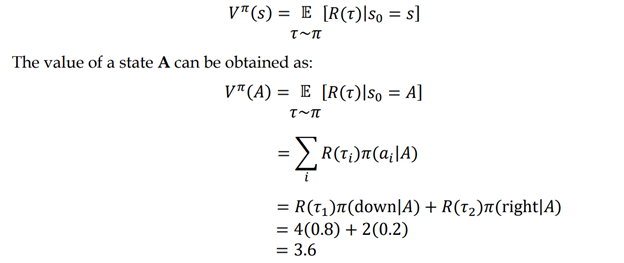
بنابراین، مقدار یک حالت بازگشت مورد انتظار مسیر است که از ان حالت شروع می‌شود.

توجه داشته باشید که تابع ارزش بستگی به سیاست دارد، یعنی ارزش state بر اساس سیاستی که انتخاب می‌کنیم متفاوت است. بسیاری از توابع ارزش های مختلف با توجه به سیاست های مختلف می‌تواند وجود داشته باشد. تابع مقدار بهینه V * (s) حداکثر ارزش در مقایسه با تمام توابع ارزش دیگر را تولید می‌کند. می توان ان را به این شکل بیان کرد:

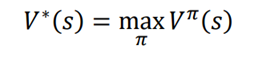
به عنوان مثال، بیایید بگوییم که دو سیاست π1 و π2 داریم. اجازه دهید برای مقدار state s سیاست Vπ1(s) = 13 استفاده شود و مقدار حالت s با استفاده از سیاست  Vπ2(s) = 11. باشد. سپس مقدار بهینه حالت s ، برابر با  V∗ (s) = 13 خواهد بود زیرا حداکثر است. سیاستی که مقدار حالت بیشینه را می‌دهد، سیاست بهینه π نامیده می‌شود.

بنابراین، در این مورد،π1 سیاست بهینه است زیرا حداکثر مقدار حالت را می‌دهد.

می‌توانیم تابع مقدار را در یک جدول به نام جدول ارزش مشاهده کنیم. بیایید فرض کنیم که دو حالت s0 و  S1 داریم. سپس تابع ارزش را می توان به صورت زیر نشان داد:

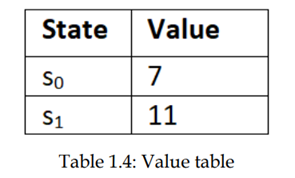
از جدول ارزش، می‌توانیم بگوییم که بهتر است در حالت s1 باشد تا حالت s0 زیرا S1 دارای ارزش بالاتر است. بنابراین می‌توانیم بگوییم که حالت s1 حالت بهینه است.

تابع Q

 تابع Q که تابع مقدار state-action نیز نامیده می‌شود، با مقدار جفت حالت - عمل را نشان می‌دهد.. ارزش جفت state-action بازدهی است که عامل با شروع از حالت s و انجام عمل تحت سیاست π.  به دست می‌اورد. مقدار یک جفت حالت - عمل یا تابع Q معمولا با Q(s,a) مشخص می‌شود و به عنوان مقدار Q یا ارزش اقدام حالت است. و به این شکل بیان شده است:

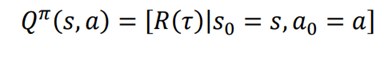
توجه داشته باشید که تنها تفاوت بین تابع ارزش و تابع Q این است که در تابع ارزش مقدار یک حالت را محاسبه می‌کنیم، در حالی که در تابع Q مقدار یک جفت state-action را محاسبه می‌کنیم.  تابع Q را با یک مثال بیشتر بشناسیم. مسیر تولید شده با استفاده از سیاست π را در شکل 1.29  در نظر بگیرید:

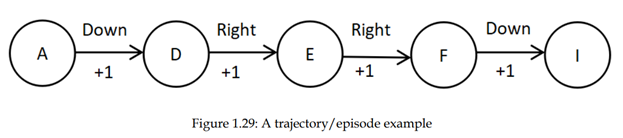
یاد گرفتیم که تابع Q مقدار یک جفت عمل حالت را محاسبه می‌کند. محاسبه مقدار Q از جفت حالت عمل A-down. یعنی مقدار Q  در حالت A در حال حرکت به پایین چند است. مقدار Q بازگشت مسیر خواهد بود که از حالت A و انجام عمل به پایین شروع می‌شود:

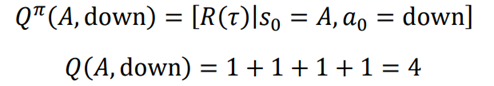
بیایید فرض کنیم که باید مقدار Q جفت عمل حالت D-right را محاسبه کنیم. که برابر مقدار Q حرکت به سمت راست در حالت D است. ارزش Q از بازگشت مسیر که از حالت D شروع می‌شود و عمل راست را انجام می‌دهد خواهد بود:

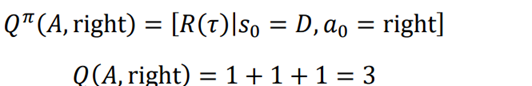
به طور مشابه، می‌توانیم مقدار Q را برای تمام جفت‌های عمل حالت محاسبه کنیم. مشابه انچه در مورد تابع ارزش یاد گرفتیم، به جای اینکه بازده را به طور مستقیم به عنوان ارزش یک جفت حالت عمل   Q در نظر بگیریم، از بازگشت مورد انتظار استفاده می‌کنیم زیرا بازگشت مقادیر مختلف با برخی از احتمال‌ها است. بنابراین، می‌توانیم تعریف مجدد عملکرد Q را به شکل زیر بنویسیم:

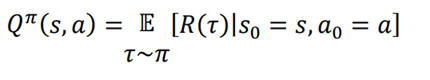
این بدان معنی است که مقدار Q بازگشت مورد انتظار است که عامل با شروع از حالت s و انجام عمل تحت سیاستπ به دست می اورد.

همانند تابع ارزش، تابع Q به سیاست بستگی دارد، یعنی ارزش Q بر اساس سیاستی که انتخاب می‌کنیم متفاوت است. و می‌تواند توابع Q مختلف وجود داشته باشد. با توجه به سیاست‌های مختلف. تابع بهینه Q تابعی است که دارای حداکثر مقدار Q نسبت به سایر توابع Q، است و می‌توان ان را به صورت زیر بیان کرد:

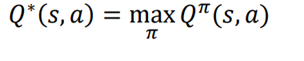
سیاست بهینه π∗ سیاستی است که حداکثر مقدار Q را می‌دهد.

مانند تابع مقدار، تابع Q را می‌توان در یک جدول مشاهده کرد.  جدول Q نامیده می‌شود. بیایید فرض کنیم که دو حالت S0 و S1 داریم و دو اقدام 0 و 1؛ سپس تابع Q می‌تواند به شرح زیر نشان داده شود:

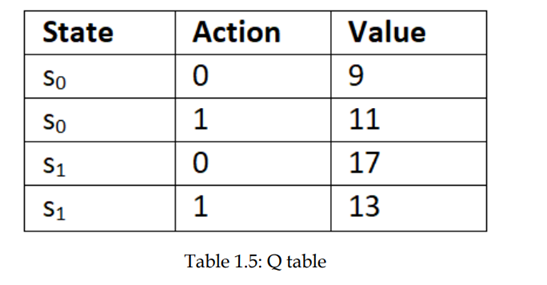
همانطور که مشاهده می‌کنیم، جدول Q نشان دهنده مقادیر Q تمام جفت حالت‌های ممکن است. یاد گرفتیم که سیاست بهینه سیاستی است که عامل حداکثر بازگشت (مجموع پاداش ها) را به دست می‌اورد. ازجدول Q ، فقط با انتخاب عملی که حداکثر مقدار Q در هر حالت را می‌دهد سیاست بهینه را تعیین کنیم . بنابراین سیاست بهینه عمل 1 در حالت s0 و عمل 0 در حالت S1 ا را انتخاب می کند زیرا دارای مقدار Q بالا هستند ، همانطور که در جدول 1.6 نشان داده شده است:

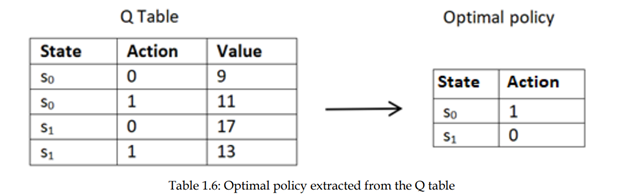
بنابراین، می‌توانیم سیاست بهینه را با محاسبه تابع Q استخراج کنیم.

منبع:

,Deep_Reinforcement_Learning_With_Python_Master_Classic_Rl,_Deep , 

Sudharsan  Ravichandiran,2020