روش برنامه نویسی پویا و بلمن

روش مبتنی بر مدل یعنی برای پیدا کردن سیاست بهینه تنها زمانی که پویایی مدل (احتمال انتقال) محیط شناخته شده است کمک خواهند کرد. اگر دینامیک مدل را نداشته باشیم، نمی‌توانیم این روش ها را اعمال کنیم.

یکی از این روش‌ها روش برنامه نویسی پویا (DP) است.

دو روش مهم که با استفاده از DP برای پیدا کردن سیاست بهینه استفاده می‌شوند را معرفی می‌کنیم . دو روش عبارتند از:

·       تکرار ارزش

·       تکرار سیاست

·       تکرار ارزش

در روش تکرار ارزش، سعی می‌کنیم سیاست بهینه را پیدا کنیم. یاد گرفتیم که سیاست بهینه ان است که به عامل می‌گوید که عمل درست را هر حالت به منظور پیدا کردن سیاست بهینه انجام دهد ، ابتدا تابع مقدار بهینه را محاسبه می‌کنیم و هنگامی که تابع ارزش مطلوب، را یافتیم می‌توانیم از ان برای استخراج  سیاست بهینه استفاده کنیم، چگونه می‌توانیم تابع مقدار بهینه را محاسبه کنیم؟ می‌توانیم از معادله بلمن بهینه برای  تابع ارزش استفاده کنیم.

·       تکرارسیاست

این مرحله دقیقا همان چیزی است که تابع مقدار را در روش تکرار ارزش محاسبه کردیم. اما با یک تفاوت کوچک. در اینجا،  تابع ارزش را با استفاده از سیاست محاسبه می‌کنیم اما در روش تکرار ارزش، ارزش را با در نظر گرفتن حداکثر مقادیر Q محاسبه می‌کنیم.

در یادگیری تقویتی، هدف این است که  سیاست بهینه را پیدا کنیم. سیاست بهینه سیاستی است که عمل درست را در هر حالت انتخاب کند به طوری که عامل حداکثر بازگشت برای  رسیدن به هدف داشته باشد.

در این فصل، با دو مفهوم یادگیری تقویتی کلاسیک جالب آشنا خواهیم شد که الگوریتم های روش های تکرار ارزش و سیاست نامیده می‌شوند که می‌توانیم از ان برای پیدا کردن سیاست بهینه استفاده کنیم.

قبل از ورود به روش‌های تکرار ارزش و سیاست به طور مستقیم، ابتدا، معادله بلمن را یاد خواهیم گرفت. معادله Bellman در یادگیری تقویتی همه جا حاضر است واز ان برای پیدا کردن مقدار بهینه و توابع Q استفاده می‌شود. ابتدا ببینیم  که معادله بلمن چیست و چگونه سیاست بهینه و توابع Q را پیدا می‌کند.

 پس از آشنایی با معادله بلمن، روش‌های برنامه نویسی پویا به نام تکرار ارزش و سیاست، که از معادله بلمن برای پیدا کردن سیاست بهینه استفاده می‌کنند را بررسی خواهیم کرد .

معادله بلمن

معادله بلمن، که به نام ریچارد بلمن نامگذاری شده است، به ما کمک می‌کند تا فرایند تصمیم گیری (MDP) مارکوف را حل کنیم. وقتی می گوییم MDP را حل کنید، منظورمان پیدا کردن سیاست بهینه است.

 معادله بلمن در یادگیری تقویتی همه جا حاضر است و به طور گسترده ای برای پیدا کردن ارزش مطلوب و توابع Q به صورت بازگشتی مورد استفاده قرار می‌گیرد.

محاسبه مقدار بهینه و توابع Q خیلی مهم است زیرا هنگامی که مقدار بهینه یا تابع Q مطلوب را داریم، پس از ان

میتوانیم از آنها برای بدست اوردن بهترین سیاست استفاده کنیم.

در این بخش، یاد خواهیم گرفت که معادله بلمن دقیقا چیست و چگونه می‌توانیم از ان برای پیدا کردن مقدار بهینه و توابع Q استفاده کنیم.

معادله بلمن تابع مقدار

معادله بلمن بیان می‌کند که مقدار یک حالت را می‌توان به صورت مجموع از پاداش فوری و ارزش تخفیف حالت بعدی بدست آورد. برای انجام یک عمل a در حالت s و حرکت به s’ حالت بعدی و سپس گرفتن  پاداش r ، معادله بلمن تابع مقدار را می‌توان به صورت زیر بیان کرد:

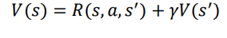
در معادله بالا، موارد زیر اعمال می‌شود:

R(s,a,s’) پاداش فوری به دست امده در حالی که انجام اقدام a در حالت s و حرکت به s’  حالت بعدی را نشان می‌دهد.

گاما عامل تخفیف است.

V(s’) به معنای ارزش حالت بعدی است. بیایید معادله بلمن را با یک مثال درک کنیم. فرض کنید یک مسیر τ با استفاده از  سیاست π تولید کنیم :

  

فرض کنیم مایلیم مقدار وضعیت s2 را محاسبه کنیم. با توجه به معادله، Bellman معادله مقدار حالت s2 به شکل  زیر می‌شود:

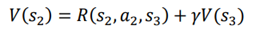
در معادله بالا، R(s2,a2,s3’)به معنای پاداش فوری است که با انجام یک عمل a2 در حالت s2 و حرکت به حالت s3. از مسیر، به دست می‌اوریم . برای راحتی پاداش فوری را r2 می‌گذاریم و عبارت γV (s3) کاهش ارزش حالت بعدی است. بنابراین، با توجه به معادله بلمن، مقدار حالت s2 به شکل زیر نمایش داده می‌شود:

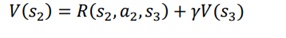
بنابراین معادله بلمن تابع مقدار را می‌توان به صورت زیر بیان کرد:

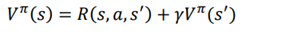
بالانویس π نشان میدهد که ما از سیاست π استفاده می‌کنیم. عبارت سمت راست معادله اغلب به عنوان پشتیبان بلمن نامیده می‌شود.

معادله بلمن قبلی تنها زمانی کار می‌کند که محیط قطعی داشته باشیم.

بیایید فرض کنیم محیط تصادفی است، سپس در این صورت، زمانی که عمل a در حالت S، انجام می‌شود تضمین نمی شود که حالت بعدی ما همیشه s’ خواهد بود  و  می تواند برخی از حالتهای دیگر نیز اتفاق بیفتد. به عنوان مثال، به مسیر در شکل 3.2 نگاه کنید.

همانطور که می‌بینیم، هنگامی که عمل a1 را انجام می‌دهیم در حالت S1 با احتمال 0.7، به وضعیت S2 و با احتمال 0.3 به حالت s3 می‌رسیم.

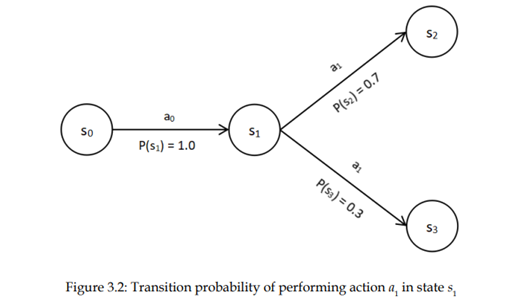
دیدیم که  معادله بلمن شامل مبلغ پاداش فوری و ارزش تخفیف حالت بعدی است. اما وقتی وضعیت بعدی به دلیل تصادفی بودن موجود در محیط تضمین نشده است. چگونه معادله بلمن را تعریف کنیم.

در این مورد، می‌توانیم معادله بلمن را با (میانگین وزنی) انتظارات کمی تغییر دهیم، یعنی مجموع پشتیبان بلمن ضرب در احتمال انتقال متناظر وضعیت بعدی باشد.

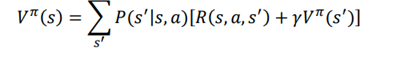
در معادله بالا، المانها عبارتند از:

  P(s’|s , a)نشان دهنده  انجام عمل a در حالت  sو  احتمال انتقال رسیدن به s’ است.

• [γVπ (s’)′  R(s,a,s) +] نشان دهنده پشتیبان Bellman است

بیایید این معادله را با در نظر گرفتن همان مسیری که قبلا استفاده کردیم بهتر درک کنیم. همانطور که متوجه می‌شوید، هنگامی که عمل a1 را در حالت S1،  انجام می دهیم به S2 با احتمال 0.70 و s3 با احتمال 0.30. می‌رویم

 بنابراین می‌توانیم بنویسیم:

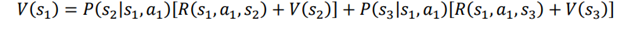
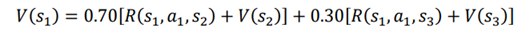
بنابراین، معادله بلمن تابع مقدار شامل محیط تصادفی با استفاده از انتظارات (میانگین وزنی) به شکل زیر بیان شده است:

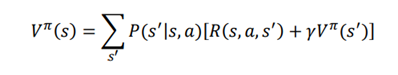
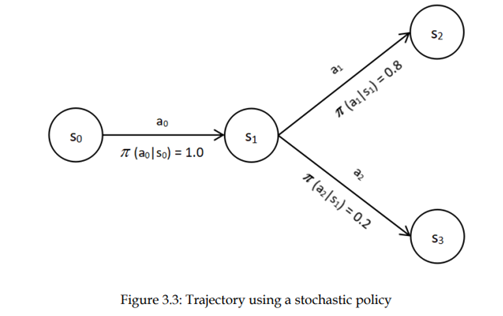
ولی اگه سیاست یک سیاست تصادفی باشه چی؟ این را با سیاست تصادفی یاد گرفتیم ، که اقدامات را بر اساس توزیع احتمال انتخاب می‌کنیم؛ یعنی به جای انجام همان عمل در یک حالت، یک عمل را بر اساس احتمال توزیع از فضای عمل انتخاب می‌کنیم. بیایید این را با  مسیر متفاوت که در شکل 3.3 نشان داده شده است درک کنیم.

همانطور که می‌بینیم، در حالت S1، با احتمال 0.8، عمل a1 را انتخاب می‌کنیم و به  حالت S2، می‌رویم و با احتمال 0.2، عمل a2 را انتخاب کرده و به حالت S3  می‌رسیم.

بنابراین، هنگامی که از سیاست تصادفی استفاده می‌کنیم، وضعیت بعدی همیشه یکسان نخواهد بود. حالت‌های مختلف با برخی از احتمالات همراه  خواهد بود. حالا، چگونه می توانیم معادله بلمن  شامل سیاست تصادفی را تعریف کنیم.

·       یاد گرفتیم که در محیط تصادفی در معادله بلمن، انتظار (میانگین وزنی) را در نظر بگیریم که مجموع پشتیبان بلمن ضرب در انتقال مربوطه احتمال وضعیت بعدی است،

·       به طور مشابه، برای گنجاندن ماهیت تصادفی سیاست در معادله،  بلمن می‌توانیم از انتظار (میانگین وزنی) یعنی یک مجموع از پشتیبان بلمن ضرب در احتمال مربوطه از عمل استفاده کنیم.

بنابراین، معادله نهایی بلمن از تابع مقدار را می‌توان به صورت زیر نوشت:

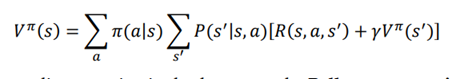
معادله بالا نیز به عنوان معادله انتظار بلمن از تابع ارزش شناخته می‌شود. همچنین می‌توانیم معادله فوق را به شکل انتظار بیان کنیم. بیایید تعریف انتظار را به یاد آوریم:

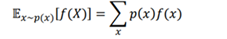
در این معادله  p(x)و  f(x) برابر است با:

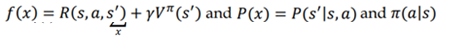
می توانیم معادله بلمن تابع ارزش را به صورت زیر بنویسیم:

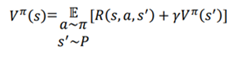
معادله بلمن تابع Q

حالا، بیایید یاد بگیریم که چگونه با معادله Bellman تابع مقدار state-action یعنی تابع Q را محاسبه کنیم، معادله بلمن تابع Q بسیار شبیه معادله بلمن تابع مقدار به جز یک تفاوت کوچک است. معادله بلمن تابع Q بیان می‌کند که مقدار Q یک جفت عمل - حالت را می‌توان با مجموع از پاداش فوری و ارزش Q تخفیف جفت حالت - عمل بعدی بدست آورد.

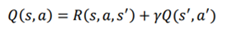
 R(s,a,s’)نشاندهنده پاداش فوری بدست آمده از عمل a برای حرکت از حالت  s به حالت s’

γ  ضریب تخفیف

Q(s’,a’) مقدار Q جفت حالت-عمل بعدی

بیایید این را با یک مثال درک کنیم. فرض کنید یک مسیر τ را با استفاده از سیاست    π داریم. همانطور که در شکل 3.4 نشان داده شده است:

فرض کنیم مایلیم که Q مقدار جفت حالت-عمل (s2,a2) را محاسبه کنیم.می توانیم طبق معادله بلمن بنویسیم:

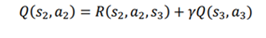
در این معادله R(s2,a2,s3) پاداش فوری که با انجام عمل a2 و حرکت از s2  به s3 را نشان می دهد.برای راحتی کار آن را با r2 نشان می دهیم. و قسمت γQ(s3,a3) تخفیف مقدار Q جفت عمل-حالت بعدی را نشان می دهد.

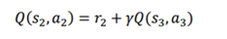
اگر از سیاست π پیروی کنیم معادله به شکل زیر نوشته می شود:

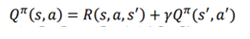
همانطور که در معادله Bellman از تابع ارزش یاد گرفتیم، معادله بلمن تنها زمانی کار می‌کند که یک محیط قطعی داشته باشیم زیرا در محیط تصادفی وضعیت بعدی ما همیشه یکسان نخواهد بود و بر اساس یک توزیع احتمالی خواهد بود. فرض کنید یک محیط تصادفی داشته باشیم، لذا زمانی که عمل در حالت S انجام دهیم حتما به حالت s’ نخواهیم رسید بنابراین مانند قبل می‌توانیم معادلات را به صورت زیر بازنویسی کنیم:

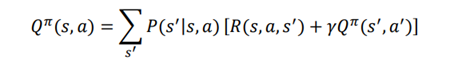
به طور مشابه، هنگامی که از یک سیاست تصادفی استفاده می‌کنیم، حالت بعدی همیشه  یکی نخواهد بود ; حالت های مختلف با احتمالات مختلف خواهد بود. بنابراین، برای ماهیت سیاست تصادفی ، می‌توانیم معادله بلمن را با انتظار (میانگین وزنی)،  بازنویسی کنیم یعنی مجموع پشتیبان گیری بلمن ضرب در احتمال عمل متناظر ، درست مثل کاری که در معادله بلمن تابع مقدار انجام دادیم. بنابراین، معادله بلمن تابع Q به صورت زیر داده می شود:

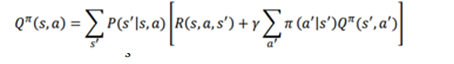
معادله بهینه سازی بلمن

معادله بهینه سازی بلمن مقدار بهینه تابع مقدار و توابع Q را نشان‌می دهد. اول، بیایید به تابع بهینه مقدار بلمن نگاه کنیم. فهمیدیم که معادله بلمن برای تابع ارزش به صورت زیر بیان می‌شود:

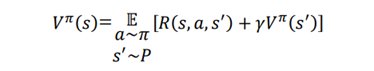
یاد گرفتیم که تابع ارزش به سیاست بستگی دارد، و ارزش حالت بر اساس سیاستی که انتخاب می‌کنیم متفاوت است. بسیاری از ارزش‌های مختلف با توجه به سیاست‌های مختلف عمل می‌کند. تابع مقدار بهینه، V∗ (s) مقداری است که حداکثر مقدار را در مقایسه با تمام مقادیر دیگر به دست می‌اورد. به طور مشابه، بسیاری از توابع مقدار Bellman مختلف با توجه به بسیاست‌های مختلف وجود دارد. تابع مقدار بهینه بلمن تابعی است که دارای بیشینه مقدار است.

خوب، چگونه می‌توانیم تابع مقدار بهینه Bellman را که دارای بیشینه مقدار است را محاسبه کنیم.

می‌توانیم تابع بهینه مقدار Bellman را با انتخاب عملی که حداکثر ارزش را نشان می‌دهد محاسبه کنیم. اما نمی‌دانیم که کدام عمل حداکثر ارزش را می‌دهد، بنابراین، ارزش حالت را با استفاده از تمام اقدامات ممکن محاسبه می‌کنیم و سپس حداکثر مقدار را به عنوان مقدار حالت انتخاب می‌کنیم.

به عبارت دیگر، از سیاست π برای انتخاب عمل استفاده کرده ، و مقدار حالت با استفاده از تمام اقدامات ممکن را محاسبه می‌کنیم و سپس حداکثر مقدار ارزش حالت را انتخاب می‌کنیم و تابع ارزش بلمن  را به شکل زیر می‌نویسیم:

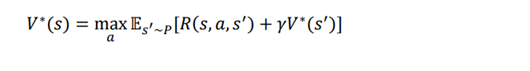
بیایید این را  با یک مثال بهتر درک کنیم. فرض کنید  در یک حالت هستیم و دو اقدام احتمالی درحالت داریم.

مثلا  اقدامات 0 و 1 باشد. سپس V∗ (s) به صورت زیر می شود:

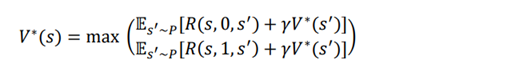
 همانطور که می توانیم از معادله بالا مشاهده کنیم، مقدار حالت را با استفاده از همه اقدامات ممکن (0 و 1) محاسبه می‌کنیم  و سپس حداکثر مقدار را به عنوان مقدار حالت انتخاب می‌کنیم.

حالا، بیایید به تابع بهینه   Q بلمن نگاه کنیم. فهمیدیم که معادله تابع Q بلمن به صورت زیر بیان می‌شود:

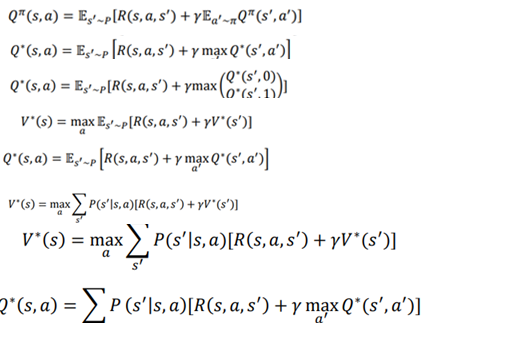
رابطه بین توابع ارزش و Q

بیایید یک مسیر انحرافی را برداریم و توابع ارزش و Q ، را مرور کنیم

·       در اصول یادگیری تقویتی. یاد گرفتیم که ارزش یک حالت (تابع ارزش) نشان دهنده بازگشت مورد انتظار است که در آن حالت پس از یک سیاست  π بدست می‌اید.

·       به طور مشابه، مقدار Q یک جفت حالت عمل (تابع Q) نشان دهنده بازگشت مورد انتظار با شروع ان جفت عمل حالت پس از یک سیاست π است.

·       یاد گرفتیم که تابع مقدار بهینه حداکثر مقدار حالت را می دهد.

·       و تابع بهینه Q حداکثر مقدار عمل حالت (مقدار Q) را نشان می‌دهد.

ایا می توانیم رابطه ای بین تابع مقدار بهینه و تابع Q بهینه بدست اوریم؟

می‌دانیم که تابع مقدار بهینه حداکثر انتظار بازگشت زمانی که از یک حالت s شروع می‌کنیم است و تابع Q بهینه حداکثر انتظار بازگشت است از زمانی که شروع به انجام  عمل a می‌کنیم. بنابراین، می‌توانیم بگوییم که تابع مقدار بهینه حداکثر مقدار Q بهینه با همه اقدامات ممکن است، و می‌توان ان را به شرح زیر بیان کرد (به عبارت دیگر، ما می‌توانیم V را از Q استخراج کنیم):

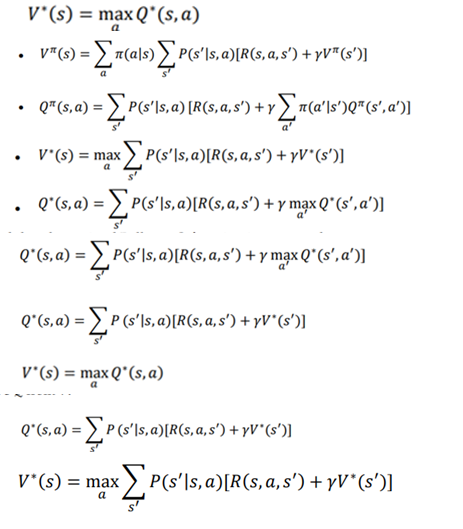
همانطور که می‌توانیم مشاهده کنیم، فقط تابع مقدار بهینه بلمن را به دست اوردیم. حالا که معادله بلمن و رابطه بین تابع  ارزش و تابع Q ،  را داریم. 

منبع:

,Deep_Reinforcement_Learning_With_Python_Master_Classic_Rl,_Deep , 

Sudharsan  Ravichandiran,2020