آشنایی با مونت کارلو

خوب، وقتی پویایی مدل محیط  را نمی‌دانیم چگونه می‌توانیم سیاست بهینه را پیدا کنیم  ؟ در چنین مواردی می‌توانیم از روش های بدون مدل استفاده کنیم.

در روش‌های بدون مدل نیازی به دینامیک مدل محیط برای محاسبه مقدار و توابع Q به منظور پیدا کردن سیاست بهینه ندارند . یکی از این روش‌های بدون مدل، روش مونت کارلو (MC) است.

روش مونت کارلو یک روش اماری است که برای یافتن راه حل تقریبی از طریق  نمونه‌برداری  استفاده می‌کند.

 

به عنوان مثال، روش مونت کارلو تقریبی از امید ریاضی یک متغیر تصادفی با نمونه برداری است، و هر چه که اندازه نمونه بیشتر باشد، تقریب بهتری خواهد شد. فرض کنیم که یک متغیر تصادفی X داریم و می‌خواهیم مقدار مورد انتظار X؛که  E (X) است را محاسبه کنیم ، می‌توانیم با در نظر گرفتن مجموع مقادیر X ضرب در احتمالات مربوطه آنها محاسبه کنیم

که به شرح زیر است:

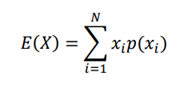
اما به جای محاسبه امیدریاضی مانند این، ایا می‌توانیم ان را با روش مونت کارلو بدست آوریم؟ بله! می‌توانیم مقدار مورد انتظار X را فقط با نمونه برداری مقادیر X برای چند بار N  تخمین بزنیم و مقدار متوسط X به عنوان انتظار محاسبه می‌شود.

مقدار X به شرح زیر است:

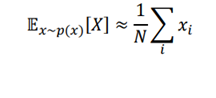
هرچه N بزرگتر باشد، تقریب بهتر خواهد بود. با روش مونت کارلو ، می‌توانیم از طریق نمونه برداری حل کنیم  و زمانی که حجم نمونه بزرگ است، تقریبی بهتر خواهد بود.

در یادگیری تقویتی، دو وظیفه مهم را انجام می‌دهیم و انها عبارتند از:

• وظیفه پیش بینی
• وظیفه کنترل

·       وظیفه پیش بینی

در وظیفه پیش بینی، یک سیاست π به عنوان یک ورودی داده می‌شود و سعی می‌کنیم مقدار تابع یا تابع Q را با استفاده از سیاست داده شده پیش بینی کنیم . اما انجام این کار چه فایده ای دارد؟ هدف این است که سیاست داده شده را ارزیابی کنیم. باید تعیین کنیم که ایا سیاست داده شده خوب یا بد است . چطور می‌توانیم اینو تشخیص بدیم؟ اگر عامل بازگشت خوبی با استفاده از سیاست داده شده داشته باشد پس از ان می‌توانیم بگوییم که سیاست خوب است. بنابراین، برای ارزیابی سیاست داده شده، باید ببینیم که عامل چه بازگشتی  از سیاست داده شده به دست می‌اورد . برای به دست اوردن بازده، تابع ارزش یا تابع Q را با استفاده از سیاست داده شده پیش بینی می‌کنیم.

·       وظیفه کنترل

            بر خلاف وظیفه پیش بینی، در وظیفه کنترل، هیچ سیاستی در ورودی داده نخواهد شد. در وظیفه کنترل، هدف پیدا    کردن سیاست بهینه است. بنابراین، با مقداردهی اولیه یک سیاست تصادفی شروع خواهیم کرد و سعی می‌کنیم سیاست بهینه را با  تکرار پیدا کنیم.

به عبارت دیگر، سعی می کنیم یک سیاست بهینه پیدا کنیم که حداکثر بازدهی را می‌دهد.

بنابراین، به طور خلاصه، در وظیفه پیش بینی، پیش بینی تابع مقدار یا تابع Q، تحت سیاست ورودی داده شده را ارزیابی می‌کنیم که کمک می‌کند تا درک کنیم که اگر ان را با استفاده از سیاست داده شده انجام دهیم، بازگشت یک عامل چه چیزی را دریافت خواهد کرد.  در وظیفه کنترل، هدف پیدا کردن سیاست بهینه است و هیچ سیاست به عنوان ورودی داده نمی‌شود; بنابراین با راه اندازی یک سیاست تصادفی شروع خواهیم کرد و سعی می‌کنیم سیاست بهینه را به صورت تکراری پیدا کنیم.

اکنون که متوجه شدیم وظایف پیش بینی و کنترل چیست، در بخش بعدی ، یاد خواهیم گرفت که چگونه از روش مونت کارلو برای انجام پیش بینی و کنترل وظایف استفاده کنیم.

·       پیش بینی مونت کارلو

در این بخش، یاد خواهیم گرفت که چگونه از روش مونت کارلو برای انجام وظیفه پیش بینی استفاده کنیم. اموخته ایم که در کار پیش بینی، به ما یک سیاست داده می‌شود و تابع ارزش یا تابع Q را با استفاده از سیاست داده شده برای ارزیابی آن پیش بینی می‌کنیم .

اول، بیایید تعریف تابع ارزش را خلاصه کنیم. تابع ارزش یا مقدار حالت را می‌توان از حالت s شروع کنیم و با پیروی از سیاست π برای  بدست آوردن بازگشت مورد انتظار عامل تعریف کرد که به شکل زیر نمایش داده می‌شود:

 

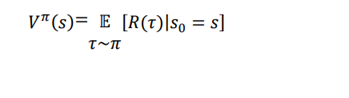
خوب، چگونه می‌توانیم ارزش حالت (تابع ارزش) را با استفاده از روش مونته کارلو تخمین بزنیم؟ در ابتدای فصل، متوجه شدیم که مونت کارلو روش تقریبی مقدار مورد انتظار یک متغیر تصادفی با نمونه برداری است، و هنگامی که اندازه نمونه بیشتر باشد، تقریب بهتر خواهد بود. ایا می توانیم از این مفهوم روش مونت کارلو برای پیش بینی ارزش یک حالت استفاده کرد؟ بله

به منظورمحاسبه  تقریبی ارزش حالت با استفاده از روش مونت کارلو، از قسمت نمونه (مسیر) تحت سیاست داده شده π برای N بار  نمونه برداری می‌کنیم و سپس مقدار حالت را به عنوان میانگین بازده یک حالت در سراسر نمونه محاسبه می‌کنیم و می‌توان ان را به شکل زیر بیان کرد:

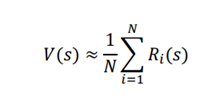
از معادله قبلی،  می‌توانیم درک کنیم که ارزش یک حالت s می‌تواند با محاسبه میانگین بازگشت حالت s از  قسمت‌های N تقریبی بدست آید. تقریب بهتر خواهد بود زمانی که N بزرگتر است.

الگوریتم پیش بینی MC

الگوریتم پیش بینی مونت کارلو به شرح زیر است:

1. total_return (s)  مجموع بازگشت یک حالت در چند قسمت است و N(s) شمارنده است، یعنی تعداد دفعاتی که یک حالت در کل قسمت‌ها بازدید می‌شود. مقداردهی اولیه total_return (s) و N(s)  برابر صفر برای همه حالتها درنظر می‌گیریم و سیاست π به عنوان ورودی داده می‌شود.

2. برای تعداد M تکرار:

1. ایجاد یک قسمت با استفاده از سیاست π

2. ذخیره تمام پاداش به دست امده در هر قسمت در لیستی به نام reward

3. برای هر مرحله t در قسمت:

1. محاسبه بازگشت st وضعیت به عنوان R (st)) = مجموع(پاداش[t:])

2. به روز رسانی کل بازگشت حالت ST به عنوان total_returns (st)) = total_return (st)) + R (st))

3. شمارنده را به عنوان N (st) به روز کنید) = N (St)) + 1

3. محاسبه مقدار یک حالت فقط با در نظر گرفتن متوسط، که برابر است:V (s) = total_return / N(s)

الگوریتم بالا  نشان می‌دهد که مقدار حالت فقط بازده متوسط از حالت در سراسر چند قسمت است.

انواع پیش بینی MC

یاد گرفتیم که الگوریتم پیش بینی مونت کارلو چگونه کار می کند.

الگوریتم پیش بینی مونت کارلو به دو نوع تقسیم می‌شود:

·       اولین بازدید مونت کارلو

·       هر بازدید مونت کارلو

اولین بازدید مونت کارلو

در روش پیش بینی MC، ارزش حالت را با فقط گرفتن بازگشت به طور متوسط از حالت در قسمت‌های مختلف بدست می‌آوریم. می‌دانیم که در هر قسمت یک حالت می‌تواند چندین بار بازدید شود. در روش اولین دیدار مونت کارلو ، اگر همان حالت دوباره در همان قسمت بازدید شود، بازگشت دوباره به ان حالت را محاسبه نمی‌کنیم . به عنوان مثال، موردی را در نظر بگیرید که در ان یک عامل بازی مارها و پله ها را بازی می‌کند اگر عامل بر روی یک مار فرود می‌اید، شانس خوبی وجود دارد که عامل به وضعیتی که قبلا از ان بازدید کرده بود باز خواهد گشت. بنابراین، هنگامی که عامل دوباره به همان حالت برود، بازده ان حالت را برای بار دوم محاسبه نمی‌کنیم.

هر بازدید مونت کارلو

همانطور که ممکن است حدس بزنید، هر بازدید مونت کارلو درست برعکس اولین بازدید مونت کارلو است. در اینجا، هر بار که یک حالت در قسمت بازدید می‌شود بازگشت آن محاسبه می‌شود.

منبع:

,Deep_Reinforcement_Learning_With_Python_Master_Classic_Rl,_Deep , 

Sudharsan  Ravichandiran,2020